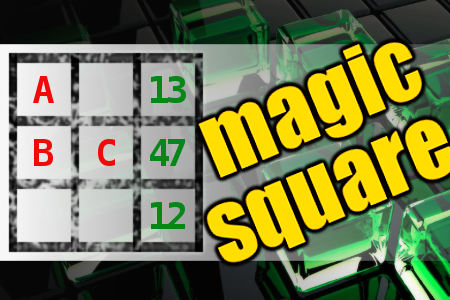
MAGIC SQUARE: Calculate A+B-C
The aim is to place the some numbers from the list (6, 9, 12, 13, 15, 19, 44, 47, 51, 73) into the empty squares and squares marked with A, B an C. Sum of each row and column should be equal. All the numbers of the magic square must be different. Find values for A, B, and C. Solution is A+B-C.Correct answers: 14
The first user who solved this task is Nasrin 24 T.
#brainteasers #math #magicsquare
I am passing this on to you be...
I am passing this on to you because it definitely works and we could all use a little more calmness in our lives. By following simple advice heard on the Dr. Phil show, you too can find inner peace.
Dr Phil proclaimed, "The way to achieve inner peace is to finish all the things you have started and have never finished."
So, I looked around my house to see all the things I started and hadn't finished, and before leaving the house this morning, I finished off a bottle of Merlot, a bottle of Zinfandel, a bottle of Bailey's Irish Cream, a bottle of Kahlua, a package of Oreos, the remainder of my old Prozac prescription, the rest of the cheesecake, some Doritos, and a box of chocolates and the rest of my half-gallon of Blue Bell Original Vanilla Bean ice-cream.
You have no idea how freaking good I feel right now. Please pass this on to those whom you think might be in need of inner peace.
Dr Phil proclaimed, "The way to achieve inner peace is to finish all the things you have started and have never finished."
So, I looked around my house to see all the things I started and hadn't finished, and before leaving the house this morning, I finished off a bottle of Merlot, a bottle of Zinfandel, a bottle of Bailey's Irish Cream, a bottle of Kahlua, a package of Oreos, the remainder of my old Prozac prescription, the rest of the cheesecake, some Doritos, and a box of chocolates and the rest of my half-gallon of Blue Bell Original Vanilla Bean ice-cream.
You have no idea how freaking good I feel right now. Please pass this on to those whom you think might be in need of inner peace.