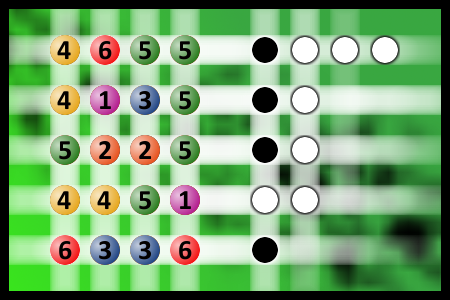
Which is a winning combination of digits?
The computer chose a secret code (sequence of 4 digits from 1 to 6). Your goal is to find that code. Black circles indicate the number of hits on the right spot. White circles indicate the number of hits on the wrong spot.Correct answers: 62
The first user who solved this task is James Lillard.
#brainteasers #mastermind
Trying to Please Mama
The first woman was elected U.S. president. She called her mom to make sure she was coming to the inauguration.
"I don’t know, dear. What would I wear?”
"Don’t worry, Mom. I’ll send a designer to help you.”
"But you know I need special foods for my diet.”
"Mom, I’m going to the president. I can get you the food you need.”
"But how will I get there?”
"I’ll send a limo, Mom. Just come!”
"OK, OK, if it makes you happy.”
The great day came, and Mama was seated with the future cabinet members. She nudged the man on her right. “See that girl, the one with her hand on the Bible? Her brother’s a doctor!”
"I don’t know, dear. What would I wear?”
"Don’t worry, Mom. I’ll send a designer to help you.”
"But you know I need special foods for my diet.”
"Mom, I’m going to the president. I can get you the food you need.”
"But how will I get there?”
"I’ll send a limo, Mom. Just come!”
"OK, OK, if it makes you happy.”
The great day came, and Mama was seated with the future cabinet members. She nudged the man on her right. “See that girl, the one with her hand on the Bible? Her brother’s a doctor!”