BRAIN TEASERS

enter your answer and press button OK

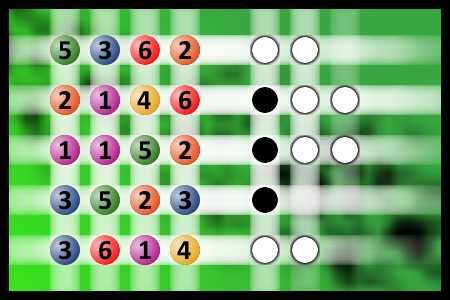
Which is a winning combination of digits?

The computer chose a secret code (sequence of 4 digits from 1 to 6). Your goal is to find that code. Black circles indicate the number of hits on the right spot. White circles indicate the number of hits on the wrong spot.

Correct answers: 58

The first user who solved this task is Sanja Šabović.

#brainteasers #mastermind

Register with your Google Account and start collecting points.

Check your ranking on list.

The most romantic story

The most romantic story isn't Romeo and Juliet who died together, but Grandma and Grandpa who grew old together.

Jokes of the day - Daily updated jokes. New jokes every day.

Follow Brain Teasers on social networks

Brain Teasers

puzzles, riddles, mathematical problems, mastermind, cinemania...

Sven Anders Hedin

Died 26 Nov 1952 at age 87 (born 19 Feb 1865).Swedish explorer and geographer who led through Central Asia a series of expeditions that resulted in important archaeological and geographical findings. During his first major Asian expedition, he crossed the Pamirs, charted Lop Nor (Lake) in China, and finally arrived at Beijing. He then journeyed to Tibet by way of Mongolia, Siberia, and the Gobi Desert. Hedin explored Tibet and Xinjiang (Sinkiang), identified the sources of the Brahmaputra, Indus, and Sutlej rivers, and, in 1906, explored and named the Trans-Himalayas. In 1927 Hedin led an expedition of Chinese and Swedish scientists into Central Asia. He wrote Through Asia (1898), The Conquest of Tibet (1935), My Life as an Explorer (1926), and other accounts of his travels.

This site uses cookies to store information on your computer. Some are essential to help the site properly. Others give us insight into how the site is used and help us to optimize the user experience. See our privacy policy.